how to draw a person in 3d perspectivr

This post is a continuation of a serial of posts well-nigh WebGL. The first started with fundamentals and the previous was about 3D Basics. If you lot haven't read those please view them first.

In the last post nosotros went over how to do 3D simply that 3D didn't have whatever perspective. It was using what's called an "orthographic" view which has its uses but it'south more often than not not what people want when they say "3D".

Instead we demand to add perspective. Just what is perspective? It'southward basically the feature that things that are further away appear smaller.

Looking at the instance above nosotros see that things further away are drawn smaller. Given our current sample 1 easy way to go far and then that things that are further away appear smaller would be to divide the prune space X and Y by Z.

Recollect of it this way: If yous have a line from (10, fifteen) to (20,fifteen) it's 10 units long. In our current sample it would be drawn ten pixels long. But if nosotros divide by Z so for example if Z is 1

10 / 1 = ten 20 / ane = 20 abs(10-20) = x        

information technology would be ten pixels long, If Z is 2 it would be

10 / ii = 5 20 / 2 = 10 abs(5 - 10) = 5        

v pixels long. At Z = three information technology would be

x / 3 = 3.333 20 / 3 = 6.666 abs(3.333 - vi.666) = 3.333        

You tin can see that every bit Z increases, as it gets further away, we'll cease upwardly drawing information technology smaller. If nosotros divide in clip infinite nosotros might get better results because Z volition exist a smaller number (-i to +1). If we add a fudgeFactor to multiply Z earlier we divide we tin can adjust how much smaller things become for a given distance.

Let'southward endeavour information technology. First allow'south alter the vertex shader to divide by Z after we've multiplied it past our "fudgeFactor".

          <script id="vertex-shader-3d" type="x-shader/x-vertex"> ... +uniform float u_fudgeFactor; ... void main() {   // Multiply the position by the matrix.   vec4 position = u_matrix * a_position;  +  // Adjust the z to divide by +  float zToDivideBy = one.0 + position.z * u_fudgeFactor;  *  // Divide 10 and y by z. *  gl_Position = vec4(position.xy / zToDivideBy, position.zw); } </script>                  

Note, because Z in prune space goes from -1 to +ane I added one to become zToDivideBy to go from 0 to +2 * fudgeFactor

We also demand to update the code to allow us set the fudgeFactor.

                      ...   var fudgeLocation = gl.getUniformLocation(plan, "u_fudgeFactor");    ...   var fudgeFactor = 1;   ...   function drawScene() {     ...     // Gear up the fudgeFactor     gl.uniform1f(fudgeLocation, fudgeFactor);      // Draw the geometry.     var primitiveType = gl.TRIANGLES;     var offset = 0;     var count = 16 * 6;     gl.drawArrays(primitiveType, kickoff, count);                  

And here's the result.

If information technology's not clear drag the "fudgeFactor" slider from 1.0 to 0.0 to see what things used to await like before we added our divide past Z code.

orthographic vs perspective

It turns out WebGL takes the x,y,z,due west value we assign to gl_Position in our vertex shader and divides it by w automatically.

Nosotros tin can prove this very easily by irresolute the shader and instead of doing the sectionalization ourselves, put zToDivideBy in gl_Position.w.

          <script id="vertex-shader-2d" blazon="ten-shader/x-vertex"> ... uniform bladder u_fudgeFactor; ... void main() {   // Multiply the position by the matrix.   vec4 position = u_matrix * a_position;    // Adjust the z to divide past   float zToDivideBy = i.0 + position.z * u_fudgeFactor;    // Dissever x, y and z past zToDivideBy *  gl_Position = vec4(position.xyz, zToDivideBy);    // Pass the color to the fragment shader.   v_color = a_color; } </script>                  

and meet how it's exactly the same.

Why is the fact that WebGL automatically divides by W useful? Because now, using more matrix magic, we can just utilise even so another matrix to copy z to west.

A Matrix like this

1, 0, 0, 0, 0, i, 0, 0, 0, 0, i, ane, 0, 0, 0, 0,          

will copy z to w. You tin can expect at each of those columns as

x_out = x_in * one +         y_in * 0 +         z_in * 0 +         w_in * 0 ;  y_out = x_in * 0 +         y_in * 1 +         z_in * 0 +         w_in * 0 ;  z_out = x_in * 0 +         y_in * 0 +         z_in * 1 +         w_in * 0 ;  w_out = x_in * 0 +         y_in * 0 +         z_in * 1 +         w_in * 0 ;          

which when simplified is

x_out = x_in; y_out = y_in; z_out = z_in; w_out = z_in;          

We can add the plus 1 nosotros had before with this matrix since we know w_in is ever 1.0.

1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, one, 0, 0, 0, 1,          

that will change the West calculation to

w_out = x_in * 0 +         y_in * 0 +         z_in * ane +         w_in * 1 ;          

and since nosotros know w_in = 1.0 then that's really

Finally we can work our fudgeFactor back in if the matrix is this

1, 0, 0, 0, 0, 1, 0, 0, 0, 0, i, fudgeFactor, 0, 0, 0, 1,          

which ways

w_out = x_in * 0 +         y_in * 0 +         z_in * fudgeFactor +         w_in * 1 ;          

and simplified that'south

w_out = z_in * fudgeFactor + ane;          

So, permit's alter the program again to just utilize matrices.

Kickoff permit's put the vertex shader dorsum. Information technology's simple again

          <script id="vertex-shader-2d" type="10-shader/10-vertex"> uniform mat4 u_matrix;  void chief() {   // Multiply the position past the matrix.   gl_Position = u_matrix * a_position;   ... } </script>                  

Next let's make a function to make our Z → W matrix.

          office makeZToWMatrix(fudgeFactor) {   return [     i, 0, 0, 0,     0, 1, 0, 0,     0, 0, 1, fudgeFactor,     0, 0, 0, i,   ]; }                  

and nosotros'll alter the code to use it.

                      ...     // Compute the matrices *    var matrix = makeZToWMatrix(fudgeFactor); *    matrix = m4.multiply(matrix, m4.projection(gl.canvas.clientWidth, gl.canvas.clientHeight, 400));     matrix = m4.translate(matrix, translation[0], translation[1], translation[ii]);     matrix = m4.xRotate(matrix, rotation[0]);     matrix = m4.yRotate(matrix, rotation[1]);     matrix = m4.zRotate(matrix, rotation[two]);     matrix = m4.scale(matrix, scale[0], scale[1], calibration[2]);      ...                  

and annotation, again, it's exactly the same.

All that was basically just to evidence you lot that dividing by Z gives usa perspective and that WebGL conveniently does this carve up by Z for u.s..

Simply there are still some issues. For example if you prepare Z to effectually -100 you'll see something like the animation beneath

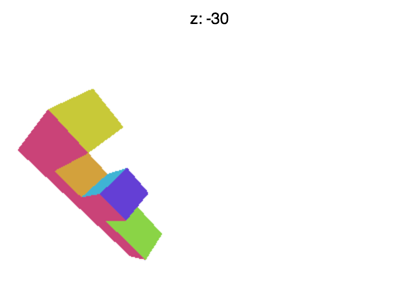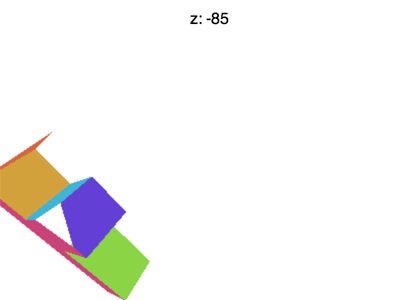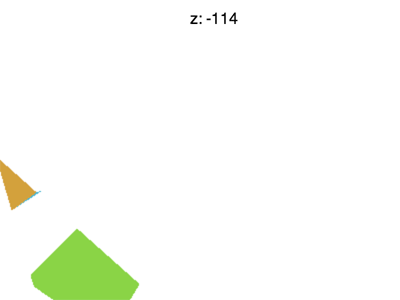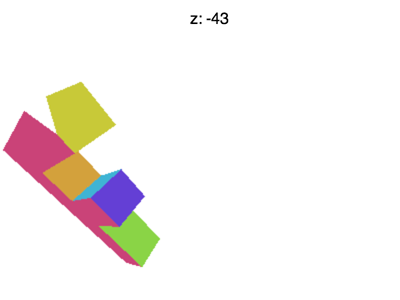
What's going on? Why is the F disappearing early on? Merely like WebGL clips 10 and Y or +i to -1 information technology as well clips Z. What nosotros're seeing here is where Z < -1.

I could become into detail about the math to set it only y'all can derive information technology the aforementioned way nosotros did 2D projection. We need to take Z, add some amount and scale some amount and we tin make any range we want get remapped to the -1 to +1.

The cool thing is all of these steps tin can be done in 1 matrix. Even better, rather than a fudgeFactor nosotros'll make up one's mind on a fieldOfView and compute the correct values to brand that happen.

Here'southward a function to build the matrix.

          var m4 = {   perspective: part(fieldOfViewInRadians, aspect, near, far) {     var f = Math.tan(Math.PI * 0.v - 0.5 * fieldOfViewInRadians);     var rangeInv = ane.0 / (virtually - far);      return [       f / aspect, 0, 0, 0,       0, f, 0, 0,       0, 0, (virtually + far) * rangeInv, -i,       0, 0, about * far * rangeInv * 2, 0     ];   },    ...                  

This matrix will practise all our conversions for us. Information technology volition conform the units and so they are in clip space, information technology volition practice the math so that we can cull a field of view by angle and it will let us cull our Z-clipping space. It assumes there'southward an heart or camera at the origin (0, 0, 0) and given a zNear and a fieldOfView it computes what it would take so that stuff at zNear ends upwardly at Z = -1 and stuff at zNear that is half of fieldOfView in a higher place or below the centre ends up with Y = -one and Y = i respectively. It computes what to use for X by but multiplying by the aspect passed in. We'd normally set this to the width / height of the brandish expanse. Finally, it figures out how much to scale things in Z and then that stuff at zFar ends up at Z = 1.

Hither'south a diagram of the matrix in action.

That shape that looks like a 4 sided cone the cubes are spinning in is called a "frustum". The matrix takes the space within the frustum and converts that to clip space. zNear defines where things volition go clipped in the forepart and zFar defines where things get clipped in the back. Fix zNear to 23 and you'll see the front of the spinning cubes become clipped. Set zFar to 24 and yous'll meet the dorsum of the cubes go clipped.

In that location'due south but one problem left. This matrix assumes there'due south a viewer at 0,0,0 and information technology assumes it'southward looking in the negative Z direction and that positive Y is upward. Our matrices up to this point have washed things in a different mode.

To make information technology appear we need to move it inside the frustum. We can exercise that by moving our F. We were cartoon at (45, 150, 0). Allow's move it to (-150, 0, -360) and allow'south set the rotation to something that makes information technology appear right side up.

Now, to use it we just need to supersede our former telephone call to m4.projection with a telephone call to m4.perspective

          var aspect = gl.sheet.clientWidth / gl.canvas.clientHeight; var zNear = 1; var zFar = 2000; var matrix = m4.perspective(fieldOfViewRadians, aspect, zNear, zFar); matrix = m4.translate(matrix, translation[0], translation[1], translation[2]); matrix = m4.xRotate(matrix, rotation[0]); matrix = m4.yRotate(matrix, rotation[1]); matrix = m4.zRotate(matrix, rotation[ii]); matrix = m4.scale(matrix, calibration[0], scale[1], scale[2]);                  

And here it is.

We're back to simply a matrix multiply and we're getting both a field of view and we're able to choose our Z space. We're not washed only this article is getting too long. Next up, cameras.

Why did nosotros move the F then far in Z (-360)?

In the other samples we had the F at (45, 150, 0) merely in the last sample it'southward been moved to (-150, 0, -360). Why did information technology need to be moved so far away?

The reason is up until this last sample our m4.project function has made a projection from pixels to clip space. That ways the area we were displaying represented 400x300 pixels. Using 'pixels' really doesn't make sense in 3D.

In other words if nosotros tried to describe with the F at 0,0,0 and not rotated nosotros'd become this

The F has its top left front corner at the origin. The projection looks toward negative Z but our F is congenital in positive Z. The projection has positive Y upward but our F is congenital with positive Z down.

Our new project only sees what's in the blue frustum. With -zNear = 1 and with a field of view of 60 degrees then at Z = -1 the frustum is but 1.154 units tall and i.154 * aspect units wide. At Z = -2000 (-zFar) its 2309 units tall. Since our F is 150 units large and the view tin simply see 1.154 units when something is at -zNear we need to move it pretty far away from the origin to run into all of it.

Moving information technology -360 units in Z moves in within the frustum. We also rotated information technology to exist right side up.

not to scale

stillerreacquink.blogspot.com

Source: https://webglfundamentals.org/webgl/lessons/webgl-3d-perspective.html

Share this post